Local surface geometry + BSDF + emission function. More...

Classes
class	ExpressiveParameters
	Non-physical manipulations of the BSDF commonly employed for expressive rendering effects. More...

class	Impulse
	A BSDF impulse ("delta function"). More...

struct	Source
	Mostly for debugging. More...

Public Types
typedef SmallArray< Impulse, 2 >	ImpulseArray
	Impulses in the BSDF. More...

Public Member Functions
	Surfel ()

virtual	~Surfel ()

virtual Radiance3	emittedRadiance (const Vector3 &wo) const
	Returns the radiance emitted by this surface in direction wo. More...

virtual Color3	finiteScatteringDensity (const Vector3 &wi, const Vector3 &wo, const ExpressiveParameters &expressiveParameters=ExpressiveParameters()) const =0
	Evaluates the finite portion of 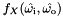$f_X(\hat{\omega_\mathrm{i}}, \hat{\omega_\mathrm{o}})$ . More...

virtual Color3	finiteScatteringDensity (PathDirection pathDirection, const Vector3 &wFrom, const Vector3 &wTo, const ExpressiveParameters &expressiveParameters=ExpressiveParameters()) const
	Provided as a convenience helper method for implementers of scatter(). More...

virtual void	getImpulses (PathDirection direction, const Vector3 &w, ImpulseArray &impulseArray, const ExpressiveParameters &expressiveParameters=ExpressiveParameters()) const =0
	Given w, returns all wo directions that yield impulses in 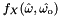$f_X(\hat{\omega}, \hat{\omega_\mathrm{o}})$ for PathDirection::SOURCE_TO_EYE paths, and vice versa for PathDirection::EYE_TO_SOURCE paths. More...

bool	isLight () const
	True if this surfel was produced by a surface that came from a Light, and thus may have emissive terms that are already accounted for by direct illumination. More...

virtual bool	nonZeroFiniteScattering () const
	True if this surfel's finiteScatteringDensity function ever returns a non-zero value. More...

virtual Color3	probabilityOfScattering (PathDirection pathDirection, const Vector3 &w, Random &rng, const ExpressiveParameters &expressiveParameters=ExpressiveParameters()) const
	Given direction w, returns the a priori probability of scattering in any direction (vs. More...

virtual Color3	reflectivity (Random &rng, const ExpressiveParameters &expressiveParameters=ExpressiveParameters()) const
	Approximate reflectivity of this surface, primarily used for ambient terms. More...

virtual bool	scatter (PathDirection pathDirection, const Vector3 &w_before, bool russianRoulette, Random &rng, Color3 &weight, Vector3 &w_after, bool &impulseScattered=ignoreBool, float &probabilityHint=ignore, const ExpressiveParameters &expressiveParameters=ExpressiveParameters()) const
	Computes the direction of a scattered photon and a weight that compensates for the way that the the sampling process is performed. More...

virtual void	transformToWorldSpace (const CoordinateFrame &xform)
	Transform this to world space using the provided xform. More...

virtual bool	transmissive () const
	Must return true if a ray is ever scattered to the opposite side of the surface with respect to the Surfel::shadingNormal. More...

Public Attributes
float	etaRatio = 1.0f
	Ratio of complex refractive indices for each side of the interface. More...

uint8	flags = 0
	0x1 = light flag More...

Vector3	geometricNormal
	The normal to the true underlying geometry of the patch that was sampled (e.g., the face normal). More...

Color3	kappaNeg
	Ratio of complex refractive indices for each side of the interface. More...

Color3	kappaPos
	Ratio of complex refractive indices for each side of the interface. More...

const Material *	material
	The material that generated this Surfel. More...

Point3	position
	Point in world space at the geometric center of this surfel. More...

Point3	prevPosition
	Point in world space at the geometric center of this surfel in the previously rendered frame of animation. More...

Vector3	shadingNormal
	The normal to the patch for shading purposes, i.e., after normal mapping. More...

Vector3	shadingTangent1
	Primary tangent vector for use in shading anisotropic surfaces. More...

Vector3	shadingTangent2
	Secondary shading tangent. More...

struct G3D::Surfel::Source	source

const Surface *	surface
	The surface that generated this Surfel. More...

Static Public Attributes
static float	ignore

static bool	ignoreBool

Protected Member Functions
	Surfel (const Point3 &position, const Point3 &prevPosition, const Vector3 &geometricNormal, const Vector3 &shadingNormal, const Vector3 &shadingTangent1, const Vector3 &shadingTangent2, const float etaPos, const Color3 &kappaPos, const float etaNeg, const Color3 &kappaNeg, const uint8 flags, const Source &source, const Material material, const Surface surface)

virtual void	sampleFiniteDirectionPDF (PathDirection pathDirection, const Vector3 &w_o, Random &rng, const ExpressiveParameters &expressiveParameters, Vector3 &w_i, float &pdfValue) const
	Called by the default implementation of scatter. More...

Static Protected Member Functions
template<class T , class ... ArgTypes>
static shared_ptr< T >	createShared (ArgTypes &&... args)
	Like std::make_shared, but works for protected constructors. More...

Detailed Description

Local surface geometry + BSDF + emission function.

The Surfel models the interface between two homogeneous media at a small patch on a surface. It is oriented, and the normal is used to give orientation to distinguish the two sides. This combines the mathematical models of a BSDF, and emission function, and a surface patch.

Scene geometric sampling functions (e.g., ray intersection) return Surfel subclasses that have been initialized with the appropriate coefficients for that location in the scene (i.e., they sample the texture map).

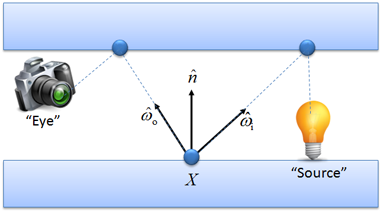
All vectors and positions are in world space. In this documentation,

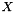is a point at which scattering (or absorption) occurs
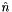$\hat{n}$ is a unit surface normal at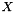
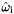$\hat{\omega}_\mathrm{i}$ is a unit vector pointing backwards along the direction that a real photon arrived a surface before scattering
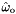$\hat{\omega}_\mathrm{o}$ is a unit vector in the direction that a real photon leaves a surface after scattering
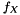is the Bidirectional Scattering Distribution Function (BSDF) at point 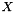, which is proportional to the probability density function describing how a photon scatters
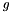is proportional to a probability density function that is used for sampling; it is ideally close to 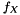to give good efficiency, but achieving that is impractical for complex BSDFs

The BSDF ( 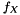$ f_X $ ) must obey the following constraints:

Normalized: 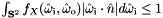$\int_{\mathbf{S}^2} f_X (\hat{\omega}_\mathrm{i}, \hat{\omega}_\mathrm{o}) |\hat{\omega}_\mathrm{i} \cdot \hat{n}| d\hat{\omega}_\mathrm{i} \leq 1$ for all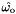 $\hat{\omega_\mathrm{o}}$
Real and non-negative everywhere
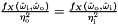
Obey the reciprocity principle $\frac{ f_X(\hat{\omega}_\mathrm{i}, \hat{\omega}_\mathrm{o}) }{ \eta_\mathrm{o}^2} = \frac{ f_X(\hat{\omega}_\mathrm{o}, \hat{\omega}_\mathrm{i}) }{ \eta_\mathrm{i}^2 }$

Most methods require a PathDirection because transmissive BSDFs are different depending on whether the path denotes a photon moving along its physical direction of propagation or a virtual path backwards from an eye. For non-transmissive BSDFs the result is the same either way.

scatter() returns a weight that compensates for distortion of the sampling distribution within the functions. When the scattering is non refractive, the caller must adjust the power or radiance scattered by this weight:

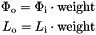
$\begin{eqnarray*} \Phi_\mathrm{o} = \Phi_\mathrm{i} \cdot \mathrm{weight}\\ L_\mathrm{o} = L_\mathrm{i} \cdot \mathrm{weight} \end{eqnarray*}$

The refractive case requires more care. If you're are tracing paths that will be connected as rays as in ray tracing or path tracing, then at a refractive interface you must adjust the radiance by:

$L_\mathrm{o} = \frac{\eta_\mathrm{i} }{ \eta_\mathrm{o}} \cdot L_\mathrm{i} \cdot \mathrm{weight}$

after invoking scatterIn or scatterOut when the path refracts. You can detect the refractive case by:

bool refracted = (sign(wo.dot(surfel->shadingNormal)) != sign(wi.dot(surfel->shadingNormal)));

However, if you're tracing paths that represent photons that will be gathered to estimate radiance by:

$L_\mathrm{o} = (\Phi_\mathrm{i} / \mathrm{gatherArea}) \cdot f_X(\hat{\omega_\mathrm{i}}, \hat{\omega_\mathrm{o}}) \cdot |\hat{\omega_\mathrm{o}} \cdot \hat{n}|$

then adjust the power after scatter() by:

$\Phi_\mathrm{o} = \Phi_\mathrm{i} \cdot \mathrm{weight}$

In this case, the divergence (or convergence) of the photons at a refractive interface will naturally be captured by the number of photons within gatherArea and no explicit correction is required.

For subclass implementers:

If it is computationally harder to importance sample than to trace rays, make the scatter functions use weights and select directions naively (e.g., uniformly). In this case, more rays will be needed for convergence because the amount of energy they contribute to the final signal will have high variance.

If it is computationally harder to trace rays than to importance sample, then it is worth spending a longer time on importance sampling to drive the weights close to 1.0, meaning that each ray contributes approximately the same energy towards convergence of the image.

Of course, the Surfel implementor cannot make these decisions in the context of a single class–they are end-to-end decisions for an entire system.

Referenced Code: Thanks to John F. Hughes, Matt Pharr, and Michael Mara for help designing this API

Member Typedef Documentation

◆ ImpulseArray

typedef SmallArray<Impulse, 2> G3D::Surfel::ImpulseArray

Impulses in the BSDF.

This contains three inline-allocated elements to support reflection and refraction without heap allocation.

Constructor & Destructor Documentation

◆ Surfel() [1/2]

G3D::Surfel::Surfel	(	const Point3 &	position,
		const Point3 &	prevPosition,
		const Vector3 &	geometricNormal,
		const Vector3 &	shadingNormal,
		const Vector3 &	shadingTangent1,
		const Vector3 &	shadingTangent2,
		const float	etaPos,
		const Color3 &	kappaPos,
		const float	etaNeg,
		const Color3 &	kappaNeg,
		const uint8	flags,
		const Source &	source,
		const Material *	material,
		const Surface *	surface
	)

protected

◆ Surfel() [2/2]

G3D::Surfel::Surfel ( )

inline

◆ ~Surfel()

virtual G3D::Surfel::~Surfel ( )

inlinevirtual

Member Function Documentation

◆ createShared()

template<class T , class ... ArgTypes>

static shared_ptr<T> G3D::ReferenceCountedObject::createShared ( ArgTypes &&... args )

inlinestaticprotectedinherited

Like std::make_shared, but works for protected constructors.

Call as createShared<myclass>.

◆ emittedRadiance()

virtual Radiance3 G3D::Surfel::emittedRadiance ( const Vector3 & wo ) const

inlinevirtual

Returns the radiance emitted by this surface in direction wo.

This models an emission function.

Defaults to zero. N.B. A "Lambertian emitter", which is often considered the ideal area light source, would return a constant value on the side

Note that this interface is intentionally insufficient for representing a point light, which requires a biradiance function.

If this function returns a non-zero value, then emissive() must return true.

Reimplemented in G3D::UniversalSurfel.

◆ finiteScatteringDensity() [1/2]

virtual Color3 G3D::Surfel::finiteScatteringDensity	(	const Vector3 &	wi,
		const Vector3 &	wo,
		const ExpressiveParameters &	expressiveParameters = `ExpressiveParameters()`
	)		const

pure virtual

Evaluates the finite portion of 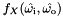$f_X(\hat{\omega_\mathrm{i}}, \hat{\omega_\mathrm{o}})$ .

This is the straightforward abstraction of the BSDF, i.e., "forward BSDF evaluation". It is useful for direct illumination and in the gather kernel of a ray tracer. Note that this does not scale the result by 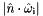$|\hat{n} \cdot \hat{\omega}_\mathrm{i}|$ .

It omits the impulses because they would force the return value to infinity.

Parameters

wi	Unit vector pointing backwards along the direction from which light came ("to the light source")
wi	Unit vector pointing out in the direction that light will go ("to the eye")

Implemented in G3D::UniversalSurfel.

◆ finiteScatteringDensity() [2/2]

virtual Color3 G3D::Surfel::finiteScatteringDensity	(	PathDirection	pathDirection,
		const Vector3 &	wFrom,
		const Vector3 &	wTo,
		const ExpressiveParameters &	expressiveParameters = `ExpressiveParameters()`
	)		const

virtual

Provided as a convenience helper method for implementers of scatter().

Allows programmatically swapping the directions (which only matters for refraction if the BSDF is reciprocal).

finiteScatteringDensity(PathDirection::SOURCE_TO_EYE, wi, wo)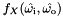 = $f_X(\hat{\omega_\mathrm{i}}, \hat{\omega_\mathrm{o}})$
finiteScatteringDensity(PathDirection::EYE_TO_SOURCE, wo, wi)=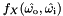 $f_X(\hat{\omega_\mathrm{o}}, \hat{\omega_\mathrm{i}})$

◆ getImpulses()

virtual void G3D::Surfel::getImpulses	(	PathDirection	direction,
		const Vector3 &	w,
		ImpulseArray &	impulseArray,
		const ExpressiveParameters &	expressiveParameters = `ExpressiveParameters()`
	)		const

pure virtual

Given w, returns all wo directions that yield impulses in 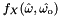$f_X(\hat{\omega}, \hat{\omega_\mathrm{o}})$ for PathDirection::SOURCE_TO_EYE paths, and vice versa for PathDirection::EYE_TO_SOURCE paths.

Overwrites the impulseArray.

For example, getImpulses(PathDirection::SOURCE_TO_EYE, wi, impulseArray) returns the impulses for scattering a photon emitted from a light.

getImpulses(PathDirection::EYE_TO_SOURCE, wo, impulseArray) returns the impulses for scattering a backwards-traced ray from the ey.

Implemented in G3D::UniversalSurfel.

◆ isLight()

bool G3D::Surfel::isLight ( ) const

inline

True if this surfel was produced by a surface that came from a Light, and thus may have emissive terms that are already accounted for by direct illumination.

◆ nonZeroFiniteScattering()

virtual bool G3D::Surfel::nonZeroFiniteScattering ( ) const

inlinevirtual

True if this surfel's finiteScatteringDensity function ever returns a non-zero value.

(May also be true even if it does only ever return zero, however).

Reimplemented in G3D::UniversalSurfel.

◆ probabilityOfScattering()

virtual Color3 G3D::Surfel::probabilityOfScattering	(	PathDirection	pathDirection,
		const Vector3 &	w,
		Random &	rng,
		const ExpressiveParameters &	expressiveParameters = `ExpressiveParameters()`
	)		const

virtual

Given direction w, returns the a priori probability of scattering in any direction (vs.

absorption), which is the directional-hemispherical reflectance and transmittance when tracing PathDirection::EYE_TO_SOURCE and hemispherical-directional reflectance and transmittance when tracing PathDirection::SOURCE_TO_EYE:

$\int_{\mathbf{S}^2} f_X(\hat{\omega_\mathrm{i}}, \hat{\omega_\mathrm{o}}) |\hat{\omega_\mathrm{o}} \cdot \hat{n}| d\hat{\omega_\mathrm{o}}.$

This method is invoked by scatter().

By default, the probability computed by sampling evaluateFiniteScatteringDensity() and getImpulses(). BSDFs that have analytic integrals can override these methods to execute more efficiently.

The return value is necessarily on [0, 1] for each frequency unless non-default expressive parameters are used.

Reimplemented in G3D::UniversalSurfel.

◆ reflectivity()

virtual Color3 G3D::Surfel::reflectivity	(	Random &	rng,
		const ExpressiveParameters &	expressiveParameters = `ExpressiveParameters()`
	)		const

virtual

Approximate reflectivity of this surface, primarily used for ambient terms.

The default implementation invokes probabilityOfScattering many times and is not very efficient.

Reimplemented in G3D::UniversalSurfel.

◆ sampleFiniteDirectionPDF()

virtual void G3D::Surfel::sampleFiniteDirectionPDF	(	PathDirection	pathDirection,
		const Vector3 &	w_o,
		Random &	rng,
		const ExpressiveParameters &	expressiveParameters,
		Vector3 &	w_i,
		float &	pdfValue
	)		const

protectedvirtual

Called by the default implementation of scatter.

Samples a directional PDF

Samples 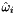$\hat{\omega}_i$ from some distribution 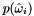$p(\hat{\omega}_i)$ on the sphere. This is optimal if proportional to 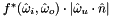$f^*(\hat{\omega}_i, \hat{\omega}_o) \cdot | \hat{\omega}_u \cdot \hat{n}|$ , where 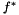$ f^* $ is the finite portion of the BSDF (no impulses) but can be anything that is nonzero where $f$ is nonzero.

Returns w_i = 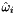$\hat{\omega}_i$ and pdfValue =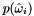 $p(\hat{\omega}_i)$

Reimplemented in G3D::UniversalSurfel.

◆ scatter()

virtual bool G3D::Surfel::scatter	(	PathDirection	pathDirection,
		const Vector3 &	w_before,
		bool	russianRoulette,
		Random &	rng,
		Color3 &	weight,
		Vector3 &	w_after,
		bool &	impulseScattered = `ignoreBool`,
		float &	probabilityHint = `ignore`,
		const ExpressiveParameters &	expressiveParameters = `ExpressiveParameters()`
	)		const

virtual

Computes the direction of a scattered photon
and a weight that compensates for the way that the the sampling process is performed.

For use in Monte Carlo integration of the rendering equation, this computes the cosine-weighted BSDF 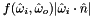$f(\hat{\omega}_i, \hat{\omega}_o) | \hat{\omega}_i \cdot \hat{n}|$ term.

The weight is needed to allow efficient computation of scattering from BSDFs that have no computationally efficient method for exact analytic sampling. The caller should scale the radiance or power transported by the weight.

For forward rays (e.g., photon tracing), call: scatter(PathDirection::SOURCE_TO_EYE, wi, ..., wo)
For backwards rays (e.g., path tracing), call: scatter(PathDirection::EYE_TO_SOURCE, wo, ..., wi)

Let h(w) be the PDF that the implementation actually samples with respect to. Let g(w) = f(w_before, w_after) |w_after.dot(n)|, the function that scatter samples. [Note: g(w) is not a PDF; just the terms from the integrand of the rendering equation]

The function produces two outputs:

w = sample with chosen with respect to pdf h(w)

weight = g(w) / h(w)

Note that the weight might be zero even if the photon scatters, for example, a perfectly "red" photon striking a perfectly "green" surface would have a weight of zero.

The probabilityHint is for use by photon mappers to decrease convergence time. If the a priori probability density of scattering in this direction was infinity, it returns 1.0. If the density was 0.0, it returns 0. For finite densities it scales between them.

If russianRoulette is true, then with probability proportional to the initial weight paths will be terminated. Nonterminated paths have weights increased proportionally to maintain the mean. (This is useful for photon mapping and pure path tracing.) The weight will be zero if the path terminates.

Note that because they are driven by the finite portion of the BSDF, weights returned must be non-negative and finite, but are not bounded. However, an efficient importance-sampling implementation will return weights close to 1.0.

The default implementation relies on getIncoming() and inefficient cosine (vs. importance) sampling against evaluateFiniteScatteringDensity(). Thus although it will work for any evaluateFiniteScatteringDensity() implementation, it is desirable to optimize the implementation of scatter() in subclasses where possible.

Consider this in the context of Monte Carlo integration of 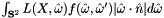$\int_{\mathbf{S}^2} L(X, \hat{\omega}) f(\hat{\omega}, \hat{\omega}') |\hat{\omega} \cdot \hat{n}| d\hat{\omega}$ . For that integral, choose 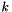$ k $ samples and weight as described below, and then multiply each by the corresponding 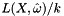$L(X, \hat{\omega}) / k$ and sum.

This is single-importance sampling based on scattering. it gives good convergence when 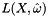$L(X, \hat{\omega})$ is uniform, and is often the best we can do and is at least correct otherwise.

Here are several different ways of implementing this method for a common example of a perfectly lambertian (f() = 1 / pif()) BRDF.

A noise-minimizing implementation:

// Direction:
w      = Vector3::cosHemiRandom(n);
//                     g(w)                          /  h(w)   
// weight = ( abs(w.dot(n)) * f(w) )                  / (abs(w.dot(n)) * 2 / (2*pif()))
// weight = ( abs(w.dot(n)) / pif() )                 / (abs(w.dot(n)) * 2 / (2*pif()))
weight = Color3::one();

Uniformly random hemisphere implementation:

// Direction:
w      = Vector3::hemiRandom(n);
//                     g(w)                          /  h(w)   
// weight = abs(w.dot(n)) * f(w))                     / (1.0 / (2.0f * pif()));
// weight = abs(w.dot(n)) * (Color3::one() / pif())   / (1.0 / (2.0f * pif()));
weight = abs(w.dot(n)) * 2.0f;

Uniformly random sphere functions:

// Direction:
w      = Vector3::random();
//                   g(w)                          /  h(w)   
// weight = abs(w.dot(n)) * f(w)                      / (1.0 / (4.0f * pif()));
// weight = abs(w.dot(n)) * (Color3::one() / pif()) * max(0, sign(w.dot(n))) / (1.0 / (4.0f * pif()));
weight = abs(w.dot(n)) * max(0, sign(w.dot(n))) * 4.0f;

There are of course a limitless number of ways of implementing the scattering.

Returns true if the weight is nonzero.

◆ transformToWorldSpace()

virtual void G3D::Surfel::transformToWorldSpace ( const CoordinateFrame & xform )

virtual

Transform this to world space using the provided xform.

◆ transmissive()

virtual bool G3D::Surfel::transmissive ( ) const

inlinevirtual

Must return true if a ray is ever scattered to the opposite side of the surface with respect to the Surfel::shadingNormal.

This may conservatively always return true (which is the default implementation). Setting this correctly doubles the efficiency of the default implementation of other methods.

There is no equivalent reflective() method because all physical transmissive surfaces are also reflective, so it would rarely be false in practice.

Reimplemented in G3D::UniversalSurfel.

Member Data Documentation

◆ etaRatio

float G3D::Surfel::etaRatio = 1.0f

Ratio of complex refractive indices for each side of the interface.

eta ( 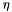$\eta$ ) is the real part, which determines the angle of refraction. kappa ( 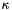$\kappa$ ) is the imaginary part, which determines absorption within the medium.

For a non-transmissive medium, eta should be NaN() and kappa should be Color3::inf().

The "Pos" versions are for the material on the side of the surface that the geometricNormal faces towards. The "Neg" versions are for the material on the side opposite the geometricNormal.

We ignore the frequency-variation in eta, since three color samples isn't enough to produce meaningful chromatic dispersion anyway.

◆ flags

uint8 G3D::Surfel::flags = 0

0x1 = light flag

The other 7 bits are reserved for future use.

Referenced by isLight().

◆ geometricNormal

Vector3 G3D::Surfel::geometricNormal

The normal to the true underlying geometry of the patch that was sampled (e.g., the face normal).

This is often useful for ray bumping.

Always a unit vector.

◆ ignore

float G3D::Surfel::ignore

static

◆ ignoreBool

bool G3D::Surfel::ignoreBool

static

◆ kappaNeg

Color3 G3D::Surfel::kappaNeg

Ratio of complex refractive indices for each side of the interface.

eta ( 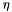$\eta$ ) is the real part, which determines the angle of refraction. kappa ( 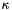$\kappa$ ) is the imaginary part, which determines absorption within the medium.

For a non-transmissive medium, eta should be NaN() and kappa should be Color3::inf().

The "Pos" versions are for the material on the side of the surface that the geometricNormal faces towards. The "Neg" versions are for the material on the side opposite the geometricNormal.

We ignore the frequency-variation in eta, since three color samples isn't enough to produce meaningful chromatic dispersion anyway.

◆ kappaPos

Color3 G3D::Surfel::kappaPos

Ratio of complex refractive indices for each side of the interface.

eta ( 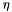$\eta$ ) is the real part, which determines the angle of refraction. kappa ( 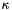$\kappa$ ) is the imaginary part, which determines absorption within the medium.

For a non-transmissive medium, eta should be NaN() and kappa should be Color3::inf().

The "Pos" versions are for the material on the side of the surface that the geometricNormal faces towards. The "Neg" versions are for the material on the side opposite the geometricNormal.

We ignore the frequency-variation in eta, since three color samples isn't enough to produce meaningful chromatic dispersion anyway.

◆ material

const Material* G3D::Surfel::material

The material that generated this Surfel.

May be nullptr. This is a raw pointer because incrementing a shared_ptr is expensive during material sampling.

◆ position

Point3 G3D::Surfel::position

Point in world space at the geometric center of this surfel.

◆ prevPosition

Point3 G3D::Surfel::prevPosition

Point in world space at the geometric center of this surfel in the previously rendered frame of animation.

Useful for computing velocity.

◆ shadingNormal

Vector3 G3D::Surfel::shadingNormal

The normal to the patch for shading purposes, i.e., after normal mapping.

e.g., the interpolated vertex normal or normal-mapped normal.

Always a unit vector.

◆ shadingTangent1

Vector3 G3D::Surfel::shadingTangent1

Primary tangent vector for use in shading anisotropic surfaces.

This is the tangent space after normal mapping has been applied.

◆ shadingTangent2

Vector3 G3D::Surfel::shadingTangent2

Secondary shading tangent.

See also: shadingTangent1

◆ source

struct G3D::Surfel::Source G3D::Surfel::source

◆ surface

const Surface* G3D::Surfel::surface

The surface that generated this Surfel.

May be nullptr. This is a raw pointer because incrementing a shared_ptr is expensive during material sampling.

Classes

Public Types

Public Member Functions

Public Attributes

Static Public Attributes

Protected Member Functions

Static Protected Member Functions

Detailed Description

Member Typedef Documentation

◆ ImpulseArray

Constructor & Destructor Documentation

◆ Surfel() [1/2]

◆ Surfel() [2/2]

◆ ~Surfel()

Member Function Documentation

◆ createShared()

◆ emittedRadiance()

◆ finiteScatteringDensity() [1/2]

◆ finiteScatteringDensity() [2/2]

◆ getImpulses()

◆ isLight()

◆ nonZeroFiniteScattering()

◆ probabilityOfScattering()

◆ reflectivity()

◆ sampleFiniteDirectionPDF()

◆ scatter()

◆ transformToWorldSpace()

◆ transmissive()

Member Data Documentation

◆ etaRatio

◆ flags

◆ geometricNormal

◆ ignore

◆ ignoreBool

◆ kappaNeg

◆ kappaPos

◆ material

◆ position

◆ prevPosition

◆ shadingNormal

◆ shadingTangent1

◆ shadingTangent2

◆ source

◆ surface